Herramienta para la selección de modelos de vectores autorregresivos estructurales
Introducción: Modelos macroeconómicos
Los modelos macroeconómicos son herramientas indispensables para la elaboración de pronósticos en cualquier banco central. Estos permiten analizar la coyuntura económica y estudiar, bajo un marco unificado de análisis, el comportamiento de las variables agregadas. Asimismo, ayudan a entender cómo los diferentes choques, ya sean internos o externos, se propagan a través de la economía y posibilitan el análisis de escenarios alternativos sobre su evolución futura. Dentro de este conjunto de herramientas, los modelos de vectores autorregresivos estructurales (SVAR) se han consolidado como un estándar del análisis económico, ya que permiten capturar las interrelaciones dinámicas entre las variables de acuerdo con su comportamiento histórico, realizar ejercicios de pronósticos y de escenarios contrafactuales de política monetaria.
En el Departamento de Investigaciones Económicas (DIE) del Banco de Guatemala (Banguat) se ha construido y desarrollado una plataforma para la selección de modelos de tipo SVAR. Esta herramienta empieza su desarrollo en 2021, inmediatamente después de que el DIE recibiera una asistencia técnica brindada por el Fondo Monetario Internacional en relación con el Modelo Macroeconómico Semiestructural (MMS)1 del Banguat. En dicha ocasión, se propuso utilizar un modelo de tipo SVAR para orientar la calibración del modelo semiestructural bajo revisión. No obstante, surgió la interrogante fundamental: ¿cómo se puede saber si un determinado modelo de tipo SVAR es una buena guía? En otras palabras, se requería un mecanismo de evaluación para este tipo de modelos. Desde entonces, se han trabajado diferentes propuestas metodológicas que pretenden cuantificar la precisión y robustez de los modelos. Este artículo presenta una propuesta concreta para responder a esta interrogante, la cual está fuertemente basada en métodos estadísticos de selección de modelos. Se inicia con una breve descripción de los modelos SVAR, abordando los métodos de estimación e identificación. Posteriormente, se describe el uso de dicha plataforma para seleccionar modelos con ciertas características de precisión y robustez.
2 ¿Qué son los modelos de vectores autorregresivos estructurales (SVAR)?
Los modelos de vectores autorregresivos (VAR) se utilizan en el análisis de series de tiempo multivariadas para modelar la interrelación dinámica de variables endógenas. En el marco de los modelos dinámicos con ecuaciones simultáneas, el modelo VAR en su forma reducida consiste en representar los valores actuales de las variables como combinaciones lineales de sus propios rezagos y de los rezagos de las demás variables incluidas en el sistema, hasta un determinado orden de rezago p. El modelo VAR en forma reducida ha mostrado ser una herramienta eficaz para describir las propiedades dinámicas de los datos, generar pronósticos, y medir la velocidad de ajuste hacia el equilibrio luego de una perturbación (Helmut Lütkepohl 2017).
Sin embargo, los modelos VAR en forma reducida no son suficientes para identificar las relaciones causales en los datos, que son clave en el análisis económico. Por esta razón, se han desarrollado los modelos VAR estructurales (SVAR, por sus siglas en inglés), los cuales incorporan relaciones estructurales fundamentadas en la teoría económica acerca de cómo interactúan las variables. Estos modelos permiten identificar los efectos causales, lo que resulta esencial para evaluar el impacto de choques económicos y realizar análisis de políticas económicas.
El modelo SVAR está dado por:
\[ B_0y_t = B_1y_{t-1} + B_2y_{t-2} + \cdots + B_{p}y_{t-p} + w_t, \quad t = 1, \ldots,T, \tag{1}\]
donde \(y_t\) es un vector de datos \(K×1\) que contiene las \(K\) variables del sistema, \(B_l,l=1,...,p\), son matrices de coeficientes de dimensión \(K×K\), la matriz \(B_0\) refleja las relaciones instantáneas entre las variables del modelo y \(w_t\) es el vector \(K×1\) de choques estructurales, los cuales no están correlacionados entre sí y cada uno posee una interpretación económica específica. Por otra parte, la representación del VAR reducido se obtiene de multiplicar por la izquierda la matriz \(B_0^{-1}\):
\[ y_t = A_1y_{t-1} + A_2y_{t-2} + \cdots + A_{p}y_{t-p} + u_t, \quad t = 1, \ldots, T, \tag{2}\]
En donde \(A_l = B_0^{-1}B_l\) y \(u_t = B_0^{-1}w_t\)
Dada una estimación de la forma reducida, lo único que se necesita para recuperar el modelo estructural Ecuación 1 es conocer la matriz \(B_0^{-1}\). Para identificar los choques estructurales \(w_t=B_0 u_t\), es necesario imponer restricciones que permitan estimar la matriz \(B_0\). El problema de encontrar restricciones económicamente adecuadas en \(B_0\) se conoce como el problema de identificación en el análisis VAR estructural (Helmut Lütkepohl 2017).
3 Estimación e identificación de modelos SVAR
La estimación de un modelo SVAR comprende dos etapas fundamentales: primero, la estimación de su forma reducida mediante el método de Mínimos Cuadrados Ordinarios (MCO); y segundo, el cálculo de su forma estructural. Este orden es crucial, ya que la forma estructural no puede estimarse directamente a partir de los datos observados. La “estructura” se refiere a la combinación de la dinámica intrínseca de la economía y los eventos exógenos e independientes (denominados “choques”), no predeterminados, que conjuntamente determinan el estado actual del sistema económico. No obstante, las variables económicas que se miden son el resultado combinado de estos dos componentes: la dinámica y los choques. Si no se conoce previamente uno de estos componentes, resulta imposible aislar el otro utilizando únicamente los datos disponibles.
Dada esta dificultad para discernir simultáneamente la dinámica y los choques a partir de los datos, el proceso de estimación del SVAR persigue dos objetivos. Primero, la estimación por MCO captura la dinámica “aparente” de los datos, es decir, la mejor proyección posible del comportamiento futuro de las variables, basada en su evolución pasada. Segundo, la identificación estructural utiliza esta dinámica aparente (obtenida mediante MCO) y la combina con restricciones impuestas por el modelador para derivar la forma estructural que sea más congruente tanto con la dinámica observada como con dichas restricciones. Es crucial destacar que estas restricciones impuestas por el modelador son exógenas a los datos y se basan en criterios externos, como la teoría económica, resultados de investigaciones previas sobre la estimación de choques, o incluso la intuición fundamentada del investigador. No obstante, no existe un consenso metodológico unificado para validar la idoneidad de estas restricciones, lo cual es un desafío que la plataforma de evaluación busca abordar.
En cuanto a la estimación de la forma reducida del VAR mediante MCO, el objetivo principal es minimizar el error (o desviación) entre los datos de la muestra y las proyecciones que el modelo VAR genera para esos mismos datos. Este proceso implica determinar la parametrización del modelo, definida por sus coeficientes representados como \(A_1,A_2,\cdots,A_p\) en la Ecuación 2, de manera que se alcance dicho mínimo. El nombre “Mínimos Cuadrados Ordinarios” (MCO) proviene, precisamente, de la métrica empleada para cuantificar este error, el Error Cuadrático Medio (ECM), y del objetivo de minimizarla. Una ventaja significativa de emplear MCO para esta estimación es la disponibilidad de una “solución analítica”, lo que significa que existe una fórmula matemática explícita para calcular directamente los coeficientes que minimizan el ECM, dados la muestra de estimación y el orden p del VAR reducido propuesto.
En lo referente a los métodos de identificación, existen diversas alternativas para imponer restricciones. Una de las más comunes es la identificación de Cholesky, que se fundamenta en ordenar las variables según su grado de exogeneidad relativa; es decir, las variables se disponen en función de su dependencia con respecto a las demás variables del modelo. Otras técnicas de identificación frecuentemente utilizadas incluyen las restricciones de largo plazo o aquellas que se basan en el aprovechamiento de los cambios en la volatilidad de las variables a lo largo del tiempo (identificación por heterocedasticidad).
Una vez impuestas las restricciones, se debe verificar si el modelo SVAR está identificado, lo que implica haber encontrado una única combinación plausible de dinámica y choques. En caso contrario (si el modelo no está identificado), es necesario reformular las restricciones. La Figura 1 resume el proceso de estimación.
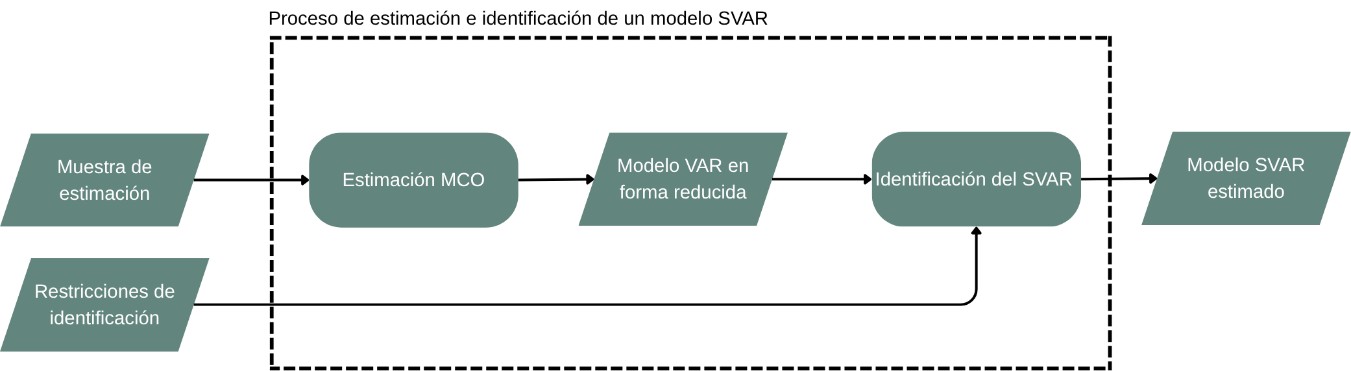
4 Herramienta de selección de modelos SVAR
La plataforma de selección de modelos permite diagnosticar la precisión de los pronósticos de corto y mediano plazo y cuantificar la relevancia de la evidencia empírica disponible que es consistente con las relaciones de causalidad postuladas por los modelos (Banco de Guatemala 2024). Es decir, los modelos se evalúan en dos dimensiones diferentes, una predictiva y una “explicativa”.
Dicha plataforma se basa fundamentalmente en la aplicación de la técnica de validación cruzada para modelos de series de tiempo. Esta técnica consiste en la conformación de múltiples submuestras a partir de los datos históricos disponibles, las cuales se emplean para estimar los parámetros del modelo. Posteriormente, dichos parámetros se utilizan para generar pronósticos sobre la porción de los datos históricos que no fue empleada en la estimación, con el propósito de construir predicciones “fuera de muestra” y así “validar” el modelo. Este ejercicio se repite para cada una de las submuestras, con el fin de cuantificar el comportamiento de los errores de pronóstico del modelo. Adicionalmente, los parámetros estimados y las relaciones de causalidad postuladas se utilizan para obtener las funciones de impulso-respuesta (IRF, por sus siglas en inglés) del modelo. De esta manera, se cuantifica la similitud de dichas respuestas a través de las diferentes submuestras de estimación.
A continuación, se describe la medición de la capacidad predictiva y explicativa de los modelos SVAR. Para ilustrar los conceptos, se presentan los resultados de un modelo derivado del proceso de búsqueda de especificaciones y selección de variables relevantes llevado a cabo en la Sección de Modelos Macroeconómicos del DIE, y que ha mostrado métricas de evaluación favorables.
4.1 Evaluación de la capacidad predictiva
La capacidad predictiva de los modelos se mide mediante un ejercicio de pronósticos fuera de muestra, en el cual se comparan los pronósticos del modelo con los valores observados en las distintas submuestras de validación. Para este procedimiento se emplea únicamente la forma reducida del modelo, es decir, el modelo VAR asociado al SVAR, sin que sea necesaria su forma estructural. Intuitivamente, basta con la dinámica capturada por el VAR para proyectar los valores de las variables.
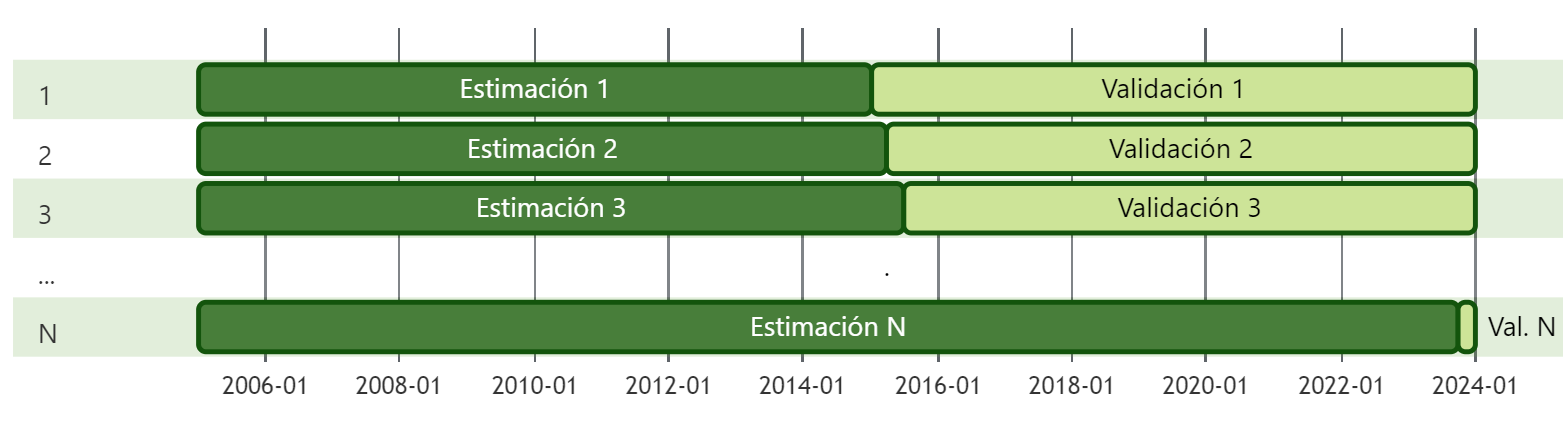
En el procedimiento de validación cruzada se definen diferentes ventanas de estimación y validación, las cuales se exploran de manera iterativa. Por ejemplo, en la Figura 2 se presenta el esquema de validación cruzada hacia adelante, en el que la muestra de estimación se expande, un trimestre a la vez, incluyendo observaciones más recientes, mientras que la muestra de validación se reduce. Por simplicidad, en este artículo se presentan únicamente los resultados de dicho esquema de validación cruzada. Sin embargo, en la práctica, se utilizan otros esquemas que complementan y robustecen los resultados.2
Dentro de cada muestra de validación, se generan pronósticos para cada uno de los horizontes posibles de manera iterada. Por ejemplo, si la primera muestra de estimación comprende 2005Q1-2014Q4 y la primera muestra de validación 2015Q1-2023Q4, entonces, el primer pronóstico a horizonte 1 corresponde a 2015Q1, al configurar el fin de historia en 2014Q4; el segundo pronóstico a horizonte 1 corresponde a 2015Q2, al posicionar el fin de historia en 2015Q1, y así sucesivamente. Este proceso se repite para los horizontes de pronóstico relevantes, empleando todas las observaciones de validación posibles.
El diagnóstico de los pronósticos se efectúa computando la raíz del error cuadrático medio (RMSE, por sus siglas en inglés) de las variables objetivo3 del modelo a diferentes horizontes. Si se tienen \(N\) iteraciones de validación cruzada, es decir, \(N\) submuestras de estimación y validación en las que es posible estimar el error de pronóstico de la variable \(i\) a un horizonte \(h\), \(\hat{e}^{(n)}_{i,h}\), entonces el RMSE está dado por la Ecuación 3. El error de pronóstico está dado por la diferencia entre los valores observados (ex-post) y los valores pronosticados por el modelo, es decir, \(\hat{e}^{(n)}_{i,h} = y^{(n)}_{i,h} - \hat{y}^{(n)}_{i,h}\) en la submuestra de validación \(n\).
\[ RMSE_{i,h} = \sqrt{\frac{1}{N}\sum^{N}_{n=1}(\hat{e}^{(n)}_{i,h})^2} \tag{3}\]
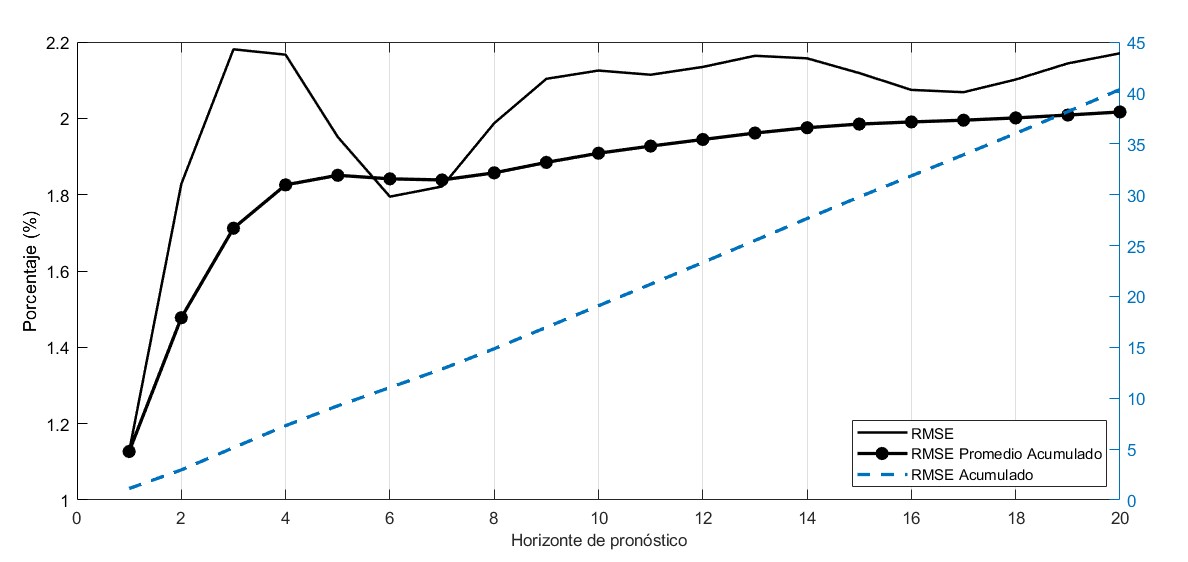
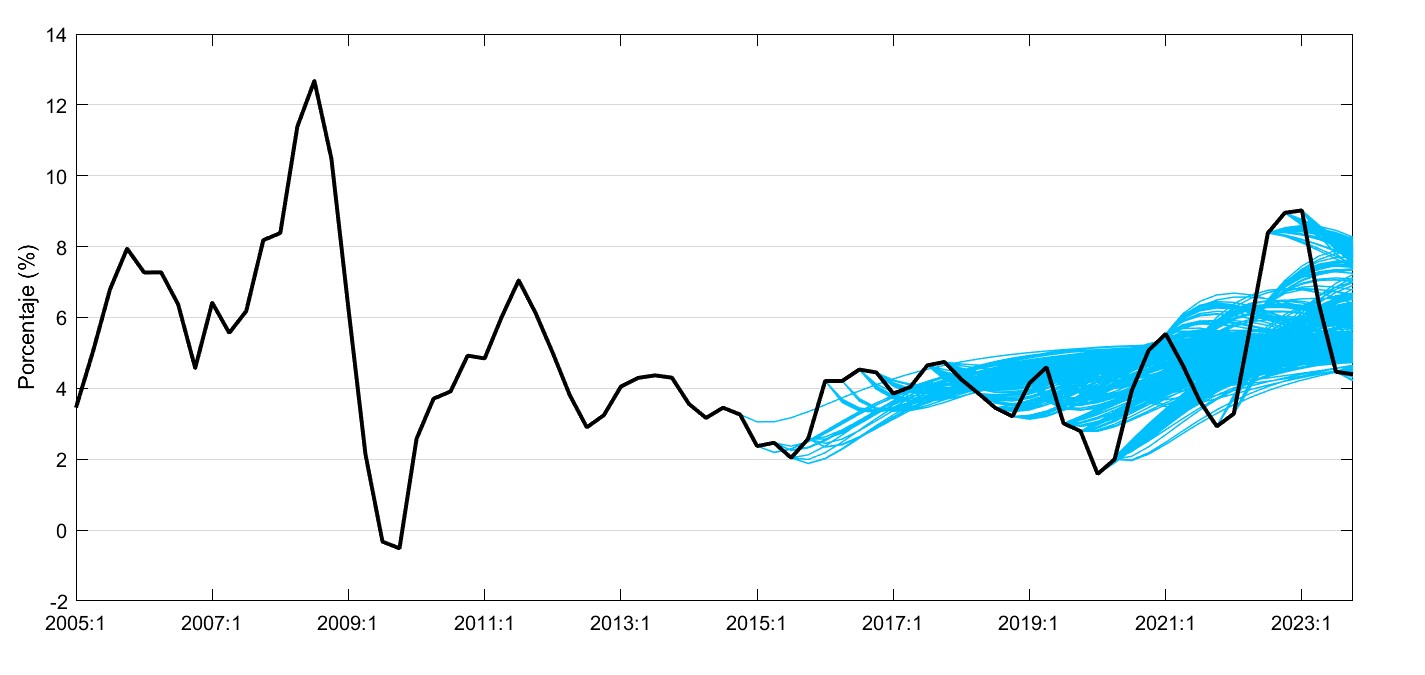
La Figura 3 (a) muestra el RMSE de la tasa de inflación interanual del modelo de ejemplo, en función de los horizontes de pronóstico. Como es de esperarse, el RMSE aumenta conforme el horizonte de pronóstico es más lejano. Principalmente, esta gráfica permite cuantificar los errores de pronóstico promedio en que incurre el modelo SVAR en cuestión. Al comparar esta gráfica con las de otros modelos, es posible observar cuál modelo resulta más apropiado para realizar pronósticos a diferentes horizontes. Por su parte, la Figura 3 (b) muestra los pronósticos generados en el ejercicio de validación de una de las variables objetivo de los modelos, la inflación interanual. Esta gráfica de “spaghetti” se utiliza como una herramienta de diagnóstico visual del modelo, pues permite observar las diferencias entre los pronósticos generados por el modelo y los datos observados de manera ex-post.
4.2 Evaluación de la capacidad explicativa
Dado que el modelo se parametriza en distintas submuestras de estimación, se genera una colección de funciones impulso-respuesta para cada una de las variables frente a diferentes choques estructurales. Las IRFs son computadas utilizando las relaciones de causalidad postuladas en el modelo estructural y los parámetros estimados de la forma reducida. La evaluación de la capacidad explicativa de los modelos se basa en la conjetura de que la robustez de las relaciones de causalidad impuestas en el modelo puede capturarse a través de la dispersión de las IRFs obtenidas en el proceso de validación cruzada. La intuición es que una menor dispersión de las IRFs sugiere que las respuestas estimadas de las variables del modelo a los choques estructurales son menos sensibles a las ventanas de datos específicas utilizadas durante la estimación. Por lo tanto, una menor dispersión puede indicar una mayor “regularidad empírica” conforme al modelo propuesto.
La Figura 4 muestra la distribución dinámica que permite caracterizar la dispersión en las funciones de impulso-respuesta de la inflación total ante un choque de una desviación estándar de la tasa de interés de política monetaria. Como se observa, las IRFs exhiben un alto grado de similitud en los primeros períodos y empiezan a esparcirse en períodos posteriores.
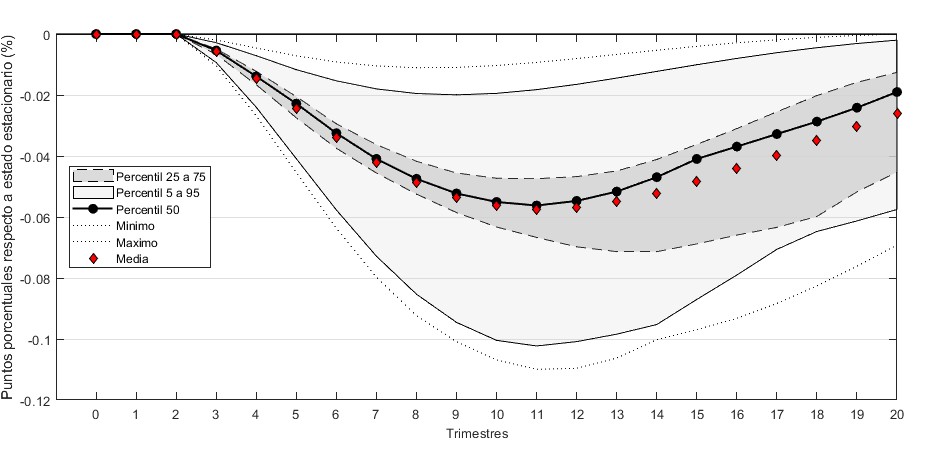
La dispersión en cada período de las IRFs es medida a través de una versión robusta del coeficiente de variación, la cual se expresa en la Ecuación 4:4
\[ CVr^{h}_{i,j} = \frac{exp(IQR^{h}_{i,j})}{exp(|m^{h}_{i,j}|)} \tag{4}\]
En donde \(IQR^{h}_{i,j}\) y \(m^{h}_{i,j}\) representan el rango intercuantílico \((Q_3-Q_1)\) y la mediana \((Q_2)\), respectivamente, de la respuesta de la variable \(i\) ante un choque en la variable \(j\) a un horizonte \(h\). Esta métrica mide la dispersión a través del rango intercuantílico y normaliza las unidades al dividir por la mediana. Ya que las respuestas decaen a cero cuando se desvanecen los choques, la mediana de las respuestas también converge a cero. Es por esto que los valores del rango intercuantílico y de la mediana son ajustados con la función exponencial.
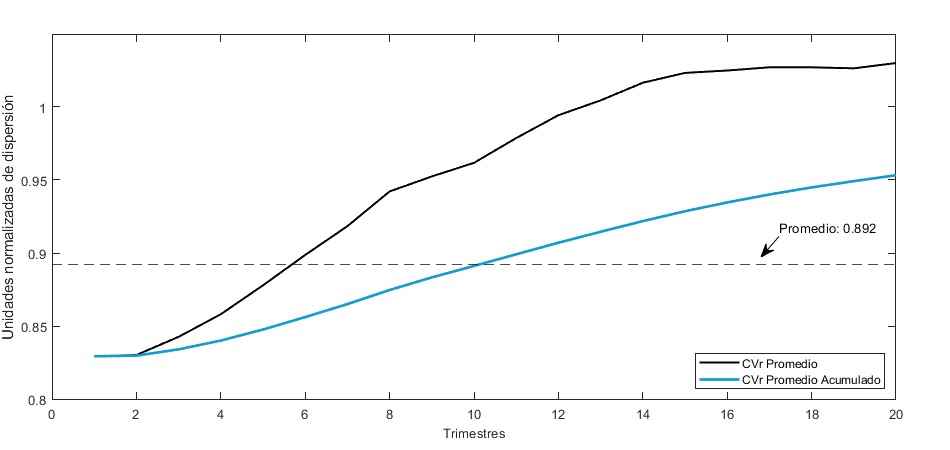
La Figura 5 muestra la medida de dispersión promedio de las funciones de impulso-respuesta de los diferentes choques hacia inflación total en los diferentes horizontes de respuesta de las IRF. Los valores menores indican una menor dispersión relativa, lo que implica una mayor consistencia de la respuesta a través de las diferentes submuestras. La gráfica muestra también el promedio acumulado, el cual se utiliza para ponderar con mayor peso los primeros horizontes de la respuesta; también se presenta el valor promedio de dispersión de 0.892, el cual se muestra en la línea horizontal punteada. Como se observa, esta medida está por debajo de la unidad para todos los horizontes de las IRFs. Esto indica que, bajo los supuestos de identificación propuestos en el modelo, se determina un bajo nivel de dispersión promedio en la respuesta de inflación ante el resto de los choques de las variables endógenas del modelo.
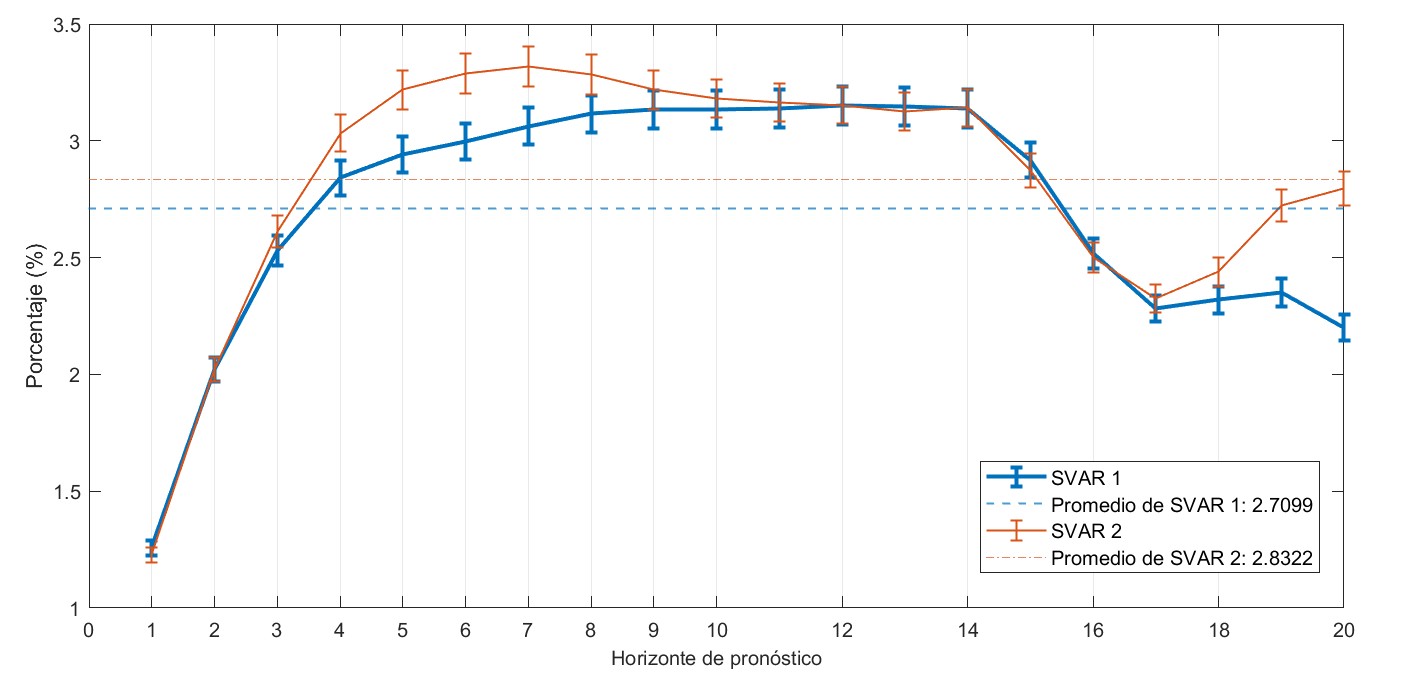
Las métricas computadas por la herramienta de selección de modelos SVAR tienen como objetivo principal facilitar la comparación entre modelos. A modo ilustrativo, las Figuras 6 y 7 presentan los resultados correspondientes a la inflación interanual en dos modelos SVAR distintos. Aunque ambos modelos incluyen esta variable, no es necesario que compartan exactamente las mismas variables endógenas o restricciones; basta con que consideren un conjunto equivalente de variables objetivo que permita su comparación.
La Figura 6 muestra el error de pronóstico para la inflación interanual. Si bien los errores son similares en ambos modelos, el SVAR 1 (línea azul) presenta errores más bajos tanto en el corto como en el largo plazo. Por su parte, la Figura 6 muestra el coeficiente de variación de las funciones de impulso-respuesta para esta misma variable. Se observa que el SVAR 1 exhibe menor variabilidad en todos los horizontes, lo que indica una mayor consistencia en las estimaciones de respuesta ante choques a lo largo de las distintas submuestras. En conjunto, estos resultados sugieren que, con base en los criterios evaluados, el SVAR 1 es preferible al SVAR 2.
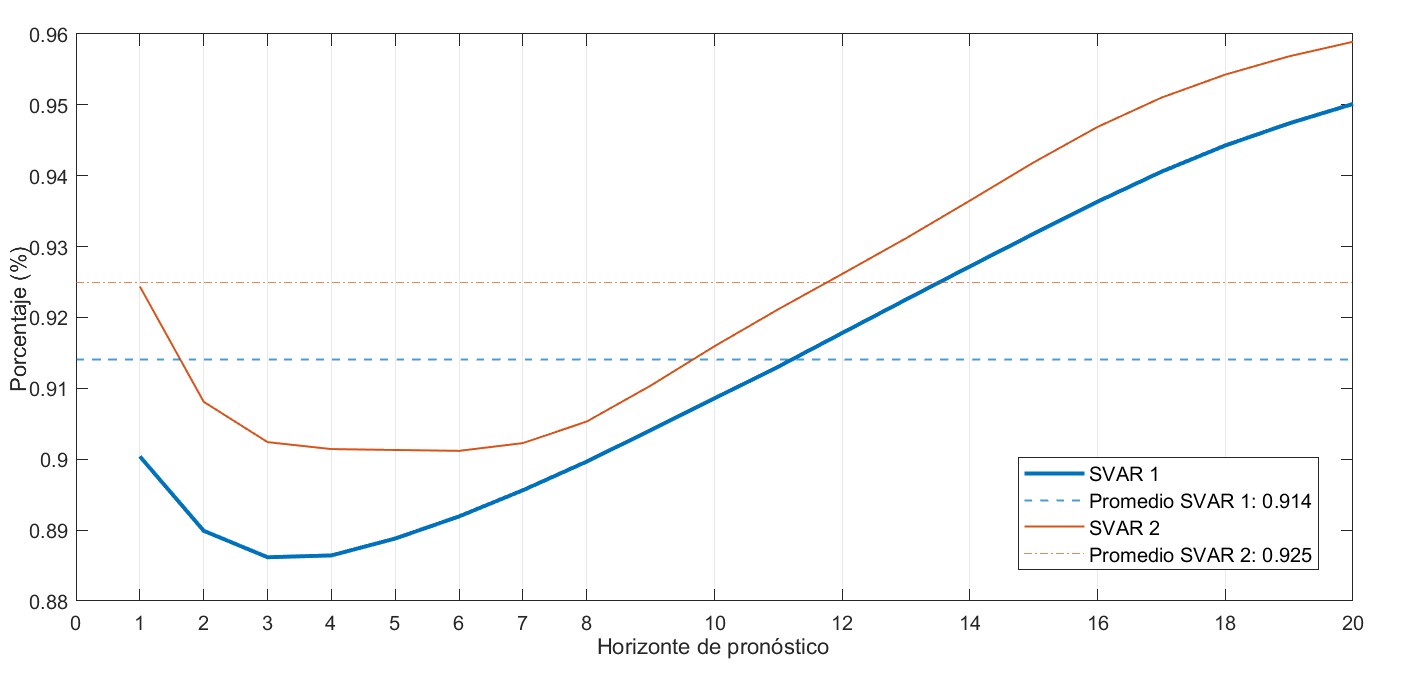
Del mismo modo, la herramienta de selección puede aplicarse a un mayor número de modelos y a distintos subconjuntos de variables objetivo, lo que permite ordenarlos según sus resultados y establecer un criterio de selección cuantitativo uniforme. No obstante, aunque estas métricas proporcionan una guía objetiva sobre el desempeño predictivo y explicativo de los modelos, su evaluación debe complementarse con criterios cualitativos fundamentales definidos por la teoría económica. Entre estos destaca, por ejemplo, la dirección esperada de las funciones de impulso-respuesta de las variables ante distintos tipos de choques, la cual debe ser coherente con la teoría económica y el conocimiento experto del funcionamiento de la economía guatemalteca.
Conclusiones
En este artículo se exponen los fundamentos de la metodología de selección de modelos SVAR empleada en el Departamento de Investigaciones Económicas del Banco de Guatemala. Esta plataforma constituye una propuesta metodológica para abordar el problema de selección de modelos macroeconómicos, considerando tanto su capacidad predictiva como explicativa. Su enfoque se basa en la extracción de la información contenida en cada una de las submuestras de estimación en las series de tiempo multivariadas, lo que significa que está profundamente basada en el análisis del comportamiento de los datos históricos. Los resultados obtenidos permiten caracterizar el error de pronóstico, así como identificar regularidades empíricas observables en las funciones de impulso-respuesta. En consecuencia, los principios incorporados en esta metodología y los resultados que se derivan de su aplicación pueden ofrecer un insumo valioso para quienes elaboran política económica con base en modelos macroeconómicos, ya sea para la generación de pronósticos de corto y mediano plazo, o para la formulación de recomendaciones de política. Sin embargo, cabe indicar que esta plataforma metodológica no debe considerarse como un producto completo y terminado, puesto que está siempre sujeta a un proceso continuo de revisión y mejora.
Referencias
Notas
El MMS no es un modelo de tipo SVAR sino más bien, como su nombre lo indica, es un modelo de tipo semiestructural; una versión estándar de este tipo de modelos ha sido desarrollada por el Fondo Monetario Internacional bajo la denominación “QPM” (o Quarterly Projection Model).↩︎
Por ejemplo, el método de ventanas móviles, expandiendo hacia atrás la muestra de estimación (backcast) y el método de validación de bloques hv. Vea Bergmeir y Benı́tez (2012) y Racine (2000) para una revisión más exhaustiva de métodos de validacón cruzada.↩︎
Las “variables objetivo” constituyen un subconjunto del conjunto de variables que integran el modelo SVAR y son aquéllas cuyos pronósticos son de particular relevancia para el usuario del modelo.↩︎
Esta medida deriva de una modificación respecto de las presentadas en Arachchige, Prendergast, y Staudte (2022).↩︎